Hertz so Good?

The resonating delusion of the 432Hz movement

Milton Mermikides ©2014
@miltonline

 

[tl;dr Kindly read at least the following 5 points before commenting:
1) I am pro-choice in terms of music, and actively encourage experimentation and challenge of the status quo in music, both in my practice and my teaching. I am also well-versed (but always learning) in terms of the science, history and multicultural practice of music.
2) This article examines all the various ‘scientific’, ‘historical’ and ‘cosmic’ arguments I have found for the superiority of the 432Hz over 440Hz tuning reference, and find them to be fallacious, contradictory, misinformed and/or unevidenced. I also see no evidence for 440Hz superiority to 432Hz (or any other over any other for that matter).
3) While there are some subtle physical world differences of 432Hz to 440Hz, I suggest that it is not a very significant musical argument to have, and there are many far better music areas of development and cultural shift (including temperament, microtiming etc.)
4) I use different tuning references, I’m very happy for anyone to do so (or anything they want to musically of course), I just am yet to find any good argument or evidence for 432Hz superiority.
5) Despite accusations to the contrary, I am not a shill of some shadowy musical establishment, Illumaniti or lizards to challenge 432Hz. Believe it or not, I’m not being paid to write this. Heaven forbid.

I welcome any critical feedback, but please keep it civil, and threats and insults to me and my family will not be tolerated. I can’t believe I have to write this about a music theory post. ]

There’s been a recent musical movement by a small but impassioned group of people advocating a change from 440Hz to 432Hz musical tuning. Proponents claim that tuning music to this frequency results in a more sonorous and ‘natural’ sound which will ultimately make every one of us happier, peaceful and healthy. Tips of how to retune music libraries and instruments abound and the benefits of the adjustment are zealously extolled by advocates. These recommendations are often accompanied by claims that the prevailing 440Hz standardization has negative effects, as well as links to Nazi Germany. The Illumaniti have also been implicated (presumably in the guise of a political powerful and wealthy musical academia) who are hiding this ‘musical truth’ which ‘they don’t want you to know”. Any popular interest in musical analysis – the enquiry into the complex and beautiful mechanics which make music work – is rare and welcome, and new ideas, subversions and revolutions are the lifeblood of musical progress. All music traditions however fossilised today are built upon revolutionary ideas of the time, so this – as any other – movement which challenges the homogeneity in musical practice, wherever they arise deserves serious consideration.

But in order to understand the effects of such a move, some basics of frequency and pitch need to be discussed, so here’s a very succinct introduction.

Frequency and Pitch

An instrument, voice – or any ‘excited’ object – will disturb the molecules in the air surrounding it, and as that object vibrates – imagine the oscillating prongs of a struck tuning fork – the molecules in the surrounding air (or whatever medium) oscillate sympathetically. Thus a wave of changing pressure propagates from the object, spreading its energy out in the surrounding air, perhaps to fall on some local ear drums (or microphone diaphragms) which in turn oscillate sympathetically. The amount the molecules are displaced is known as the amplitude and is related to our experience of volume, but here we are more concerned with the frequency of the waves: the time for each vibration cycle of the object to be completed (for example how often the prongs of our tuning fork move from their rightmost extent, bounce back and forth and return to the rightmost extent). The frequency of this oscillation is usually measured in Hertz (Hz.) the number of these cycles per second (or kHz for 1000s of cycles per second) and when these fall in the approximate range of 20Hz-20kHz we humans experience them as sound, with the frequency value correlating to pitch. The lower the frequency, the lower the pitch, the higher frequencies are heard as higher pitches. Crucially, this frequency is continuous – we can have theoretically create any frequency (and pitch) at whatever increment (440Hz, 440.02Hz, 893.3482Hz whatever) it is not stepped – although there is a perceptual limit to fine difference. It’s also important to understand that our experience of frequency is logarithmic, we hear multiplications and divisions (rather than additions and subtractions) of frequency as similar musical intervals. For example, a doubling (or halving) of a frequency creates a musical interval known as an octave, which has a sense of musical equivalence (this phenomenon is sometimes referred to as the Law of Octave Equivalence). Incidentally, doubling (or halving) a frequency is equivalent to halving (or doubling) a string length and that’s why for example you’ll find an octave exactly halfway along a guitar string.

Almost all musical cultures share the concept of the octave and give the same note names to pitches whose frequencies are multiples (or divisions) of 2. So if concert A is at 440Hz, we’ll find an infinite number of theoretical As (although only 10 or so audible ones) at 880Hz, 1.76kHz, 3.52kHz etc. above and 220Hz, 110Hz, 55.5Hz etc. below.

Slicing the Octave

So by halving or doubling we can create octaves, but other musical intervals can also be created by multiplying (or dividing) by numbers other than 2. In fact by multiplying a frequency by various frequency ratios the octave itself can be sliced into any number of subdivisions. How an octave is divided in music theory and practice is hugely interesting, complex and musically relevant with an early history that includes Ancient Babylon, Pythagoras and the Arabic world resulting in a staggering number of systems from the 22 Hindustani shrutis, 55-division Classical tuning, Javanese Slendro and Pelog, the 15(+) divisions of the Arabic maqam, Blues microtones, Harry Partch’s 43-note universe and innumerable other intuited or theoretically grounded systems.

The system many of us have inherited – at least conceptually – divides the octave into 12 equal parts (that is, each increment is based on a fixed multiplication of a reference pitch). In this 12 tone equal tempered (12-TET) system we can calculate the 12 notes by multiplying a reference pitch (usually 440Hz) by this fixed frequency ratio (the 12^th root of 2 ≈1.059463) to create a series of pitches (see below). Incidentally these fixed multiplications are associated with corresponding fixed divisions of a wavelength, and that is why you’ll notice the frets of a standard guitar fretboard get closer together as you progress up the string – each fret is placed at about 5.95% of the remaining string – not at fixed distances throughout.  The resulting pitches can be repeated at any number of octaves above (or below) by doubling (or halving) the relevant frequencies.

 

12-TET	Frequency (Hz) 440Hz Reference	Frequency relationship to reference (440Hz)
A	440	1
A# or Bb	466.16376	1.05946
B	493.88330	1.12246
C	523.25113	1.18921
C# or Db	554.36526	1.25992
D	587.32954	1.33484
D# or Eb	622.25397	1.41421
E	659.25511	1.49831
F	698.45646	1.58740
F# or Gb	739.98885	1.68179
G	783.99087	1.78180
G# or Ab	830.60940	1.88775
A’	880	2

Table 1: Absolute frequencies (and frequency relationships) of 12-TET (Concert A to the octave above) in 440Hz. All numbers approximated to 5 decimal places.

12-TET has some specific merits and many shortfalls, simplistically it excels at providing a simple system for handling complex chords and changing keys and hence became standard in the transition from Classical to Romantic music and its ultimate – and perhaps inevitable – ascent (some say descent) into 12-tone serialism. However, 12-TET ignores the spectrum of alternative divisions of the octave including those based on ‘just’ or ‘pure’ frequency ratios such as 3/2, 5/4 (as favoured in the monophonic drone based Hindustani music for example). In fact 12-TET is just one of many possible tuning systems available which have been, are, or could be put into musical practice. It is rarely questioned and many people (including musicians) blindly accept this method of octave division, wholly unaware either that other systems exist or that 12-TET is relatively new in the history of Western Art music, for example we know that Mozart considered enharmonics such as G# and Ab (which are equivalent in 12-TET) to be differently pitched notes. If one is looking for a cultural blindspot against which to rail, 12-TET is the perfect candidate. Other tuning systems are theoretically beautifully, historically and stylistically diverse and startlingly effective and relevant. If you are into a ‘revolution of consciousness’ (as the 432Hz movement purport to offer) then engage with music which eschews 12-TET: the tuning of Hindustani ragas (based on simple ‘pure’ frequency ratios of 3/2, 5/4, 6/5 and the like), the harmonic series exploitation in Tuvan throat singing, Javanese Gamelan, Murail’s spectralism, Lucy tuning’s ‘squaring the circle’ approach to 5ths and 3rds, Partch’s 11-limit universe, Taiwanese 7-TET flute and stretched octave tuning for starters.

So what ‘musical truth’ are the 432Hz proponents offering?

A New Reference

The 432Hz proponents suggest that the A reference point (often called concert A, the A above middle C on the piano, and the familiar orchestral tuning note) should be tuned not to 440Hz but to 432Hz. It’s about 31.8% on its way down to the next equal-tempered chromatic note (about 32 cents in music tuning jargon – around one third of a semitone). When one ‘tunes to 432Hz’ all the other pitches move down. So for example, the A above concert A which was previously at 880Hz (double of 440Hz, creating the octave above) now moves down to 864Hz, as do all the other 12 notes in every octave (in a 12-tone per octave system). In fact the whole network of relationships, the spectrum of frequency relationships to that reference pitch moves down.

 

12-TET	Frequency (Hz.) 440Hz Ref	Frequency relationship to reference (440Hz)	Frequency (Hz.) 432Hz Ref	Frequency relationship to reference (432Hz)
A	440	1	432	1
Bb	466.16376	1.05946	457.68806	1.05946
B	493.88330	1.12246	484.90360	1.12246
C	523.25113	1.18921	513.73747	1.18921
C#	554.36526	1.25992	544.28589	1.25992
D	587.32954	1.33484	576.65082	1.33484
D#	622.25397	1.41421	610.94026	1.41421
E	659.25511	1.49831	647.26866	1.49831
F	698.45646	1.58740	685.75725	1.58740
F#	739.98885	1.68179	726.53450	1.68179
G	783.99087	1.78180	769.73649	1.78180
G#	830.60940	1.88775	815.50741	1.88775
A	880	2	864	2

Table 2: Comparison of Frequencies and their relationships of 440Hz and 432Hz tuning. All numbers approximated to 5 decimal places.

This is an important point to make – and one many 432ruthers do not seem to understand – everything moves along with the frequency relationships. It’s like moving a Rembrandt painting a fraction of an inch down a wall and claiming an improvement. All the notes have moved, but the frequency relationships between them are identical (Table 2). [Another – perhaps better – analogy might be a small uniform decrease in the saturation of all colours in a painting]. Even though some buzz words concerning tuning systems (temperance, pure 5ths, cycles and spirals of 5ths, fundamental, just intonation etc.) appear in the word-salad of 432Hz proponent sites and posts, few show an understanding of the concept, let alone offer relevant alternatives to 12-TET tuning systems. Certainly transposing everything down to 432Hz alone will not alter any internal frequency relationships – the essence of tuning. Changing a tuning system is significant, changing a reference pitch is not necessarily so. One could argue that a reference pitch (as opposed to a tuning system or temperament) is more about the arbitrary naming of pitches, than the more pertinent interrelationship between them. The 432Hz movement lay claim to a musical enlightenment yet ironically, many accept without the question the highly conventional (and mainly ‘Western’) 12 tone division and 7 note names, and erroneously conflate a poor grasp of tuning systems with that of reference frequencies. And crucially, even when 432Hz recommend ‘just’ intonation or other alternatives to 12-TET, one must remember that 432Hz has no monopoly on these systems, which may (and are) implemented with any other reference frequency (including 440Hz).

The Arguments for 432Hz Examined

So what difference will changing a reference pitch make, and why is 432Hz specifically promoted? Let’s take some of the key arguments in turn.

1) 432Hz sounds more relaxed/seated/centered/peaceful etc. than 440Hz

Play any higher tone followed by a slightly lower one and you can convince yourself and others that the second is more relaxed and resolved, and less ‘harsh’. This is simply a trick of associating negative connotations to higher pitches and positive ones to lower pitches. A higher pitch could be described as harsh, cerebral, brash, brittle and sterile (as opposed to soft, spiritual, peaceful, relaxed and warm) or strong, thoughtful, brave, optimistic and bright (as opposed to weak, thoughtless, cowardly, pessimistic and dull). Our expectations do the rest. If you value anecdotes, then consider this: I’ve discussed the 440Hz/432Hz issue and played the two tones to an audience, almost all agree that the latter sounds more ‘relaxed’ and ‘peaceful’.  However it’s then revealed that what was actually heard was 432Hz followed by a 424.15Hz tone (a drop in pitch proportional to 440Hz-432Hz).

2) Frequency is important and 432Hz is a special number of cosmic significance

This is the most common argument for the shift to 432Hz but fails to acknowledge some basic errors of judgment. Firstly although frequency is central to musical pitch (as well as rhythm and timbre of course) it is no more important in a 432Hz than a 440Hz setting (or with any other reference point you wish to choose). Secondly, although frequency as a concept is vital, the measuring system we use (Hz: cycles per second) is entirely arbitrary, based on the various measurements available for the Earth’s – not entirely consistent -rotation period. Most recently a specific number of radiation periods of a particular atom at a specific temperature is used as the calculation. There is nothing natural or axiomatic about the number of periods, or the atom and temperature chosen. In addition 432ruthers show a complete obsession with integers, when the decimal numbering system we use is neither natural nor cosmic. Pi and Phi (as ‘naturally occurring’ numbers as one can hope to find) don’t conform to such rational niceties. The onus is on the 432Hz proponent to demonstrate any reason to accept this number over any other and have yet to come close to evidence. Embarrassing arguments about Saturn’s 864 ‘year’ (432×2) procession are approximate, data-mined and irrelevant. Saturn is argued to be the Solar System’s (and hence the Universe’s presumably) time-keeper as it is the furthest planet from the Sun. Which it is of course, not. Links of 432Hz to the ‘Earth frequency’ are examined later.

3) 432Hz is a ‘good’ frequency and tuning to 432Hz makes all the related notes ‘better’

If we accept that 432Hz is somehow better a frequency than 440Hz, then let’s look more critically at what would result from such an adjustment. 432Hz would only be the frequency of the (arbitrarily named) concert A, the other notes would be (presumably 12-TET) multiplications of that frequency, are these special also?

The argument sometimes touted that 432Hz produces more integer frequencies than 440Hz, is patently untrue (see the table above) and irrelevant even if it did. If we are so generous as to suggest that proponents mean that more integers are produced when using the 22-Shruti ‘just intonation’ tuning system, 432Hz fares a little better than 440Hz (12 of 22 vs 10 of 22 integers) but worse than other reference notes like 400Hz, 600Hz or even 622.08kHz the latter of which has all divisions as integers.

It gets worse. Just because we use a 432Hz reference doesn’t mean that that frequency is prominently represented in a piece of music. A piece entirely in the keys of B major, F# major, Eb major, Ab major, Db major among others will have no A notes in them, and other keys will have more prominent frequencies than 432Hz (and its octave equivalents).

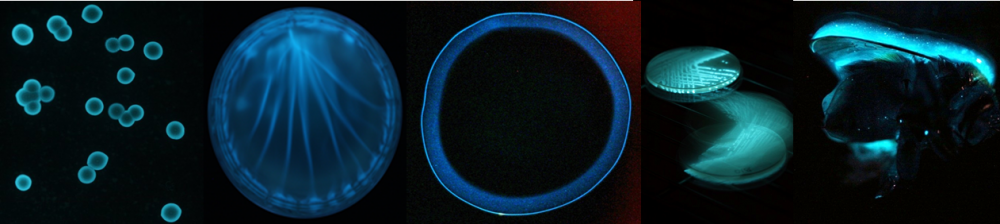
And it gets worse still. When a note is played we hear the fundamental pitch, together with a pattern of higher harmonics above it (an electronically generate sine wave is the only instrument which doesn’t exhibit this property) and that contributes to how we say, differentiate a C played on a flute to the same note on a piano. These harmonics are found at clearly differentiated and ordered intervals on melodic instruments, and more smeared across a range of frequencies in percussive instruments and ‘noisier’ sounds. The upshot of this is the following: In reference systems other than 432Hz (including the evil 440Hz), the specific frequency of 432Hz (and associated multiplications) will be heard repeatedly, presumably making it better. Conversely all those nasty frequencies found in a 440Hz reference system will be amply represented in 432Hz tuned music. Most inconvenient. Comparing a piece of music tuned from 440Hz to 432Hz (Figure 1) shows little difference in harmonic content or prominence of the ‘magic’ frequencies.

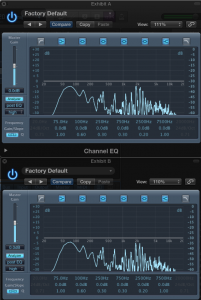
Figure 1: If you look closely you can probably tell which of these identical pieces of music is in 440Hz and which is in 432Hz. Are there any salient differences in harmonic spectrum?

4) 432Hz links to other auspicious frequencies

Claims that a 432Hz system produces the precise magic integer of 256Hz in a C below, are false. It’s close but that’s not good enough if you want to make the argument from exact integers, which is baseless anyway.

The argument from the ‘cosmological significant’ 108Hz (2 octaves below 432Hz) collapses quickly. Here’s the argument: 108 is cosmological significant because it is the distance of the Earth to the Sun divided by the Sun’s diameter (actually it’s 107.5) and also the distance of the Moon to the Earth divided by the Moon’s diameter (a way off at 110.63), so therefore 432Hz is cosmologically better. Four problems
1) The maths is wrong – or so approximate that you could make the same argument for 430.2Hz (or 442.5Hz)
2) Those 2 very provincial celestial bodies are no more cosmologically significant than the billions of others from which to choose, and the equation arbitrary
3) There’s no reason why a distance/diameter ratio – which would seem to be about gravity and relative density – should have bearing on the arbitrary time-slicing of the Hz.
4) Even if problems 1-3 somehow disappeared, there’s no reason for that number to make better music.

Don’t look behind the curtain.

Another argument – which is perhaps the most interesting – is that 432Hz produces a C# two octaves below at precisely 136.1Hz (very close but not exactly, you’d need a reference frequency of about 432.09Hz for that in 12-TET- more on that later). Why 136.1Hz? Well this is the ‘Earth frequency’  found in the Om tuning fork and is used to tune the drone note of a Sitar in Hindustani music. It is derived from the (first decimal approximation) of the frequency of the earth’s rotation around the Sun scaled up by 32 octaves (let’s not mention the complexities and competing systems of calculating a year). Rather beautiful – it doesn’t employ the fallacy of integers (only the fallacy of single decimal points) or the trappings of manufactured time units. If a reference point is arbitrary you may as well think big. It’s a rather localized geo/heliocentric view of the Universe (we could just as well use the frequency of star formations, galactic spin, cometary orbits and so forth), but if it gives one a layer of awe while engaged with music that’s all good. The implication is that it resonates in harmony (read ‘simple frequency ratio’) with the Earth’s orbit.

But there is a serious issue which arises when attempting to link it with 432Hz tuning.

Remember that there is an ethos here of harmonic rational relationships, from the Earth’s orbit to 136.1Hz. However let’s look at the relationship between 136.1Hz and the proposed 432Hz reference. Sure it’s very close to a 12-TET C# in 432Hz tuning, but this yields a wholly unwieldy 1.26018518518519 ratio (adjusting for octaves) a wasteland – or tenuous approximation – of a ‘pure’ frequency ratio. If we accept that sort of level of harmonic elegance then there are countless other reference points we might choose, and many far better. So 432Hz is linked is 136.1Hz only via the standardized ‘western’ 12-TET system, hardly a claim to an ancient harmonic truth. It’s a henna tattoo of a claim to authenticity. Sure one could use a 432hz reference and 12-TET to ‘find’ a close approximation to 136.1Hz on a C# but then if you wanted to make pure intervals from that fundamental, 432Hz would not be one of those ‘pure’ related intervals. In fact the equal-tempered major 3rd (the interval found between A and C#) is a fundamental problem with 12-TET and why musicians and theorists have for years worked on ways to make 3rds sonorous with a limited set of pitches. As it stands the 12-TET major 3^rd is way sharper than the pure third (5/4) which is implemented in musical performance where pitches can be freely altered (Indian classical music, string ensemble, vocal choirs etc.) and flatter than the ‘Pythagorean third’ of 81/64. In short 432Hz and 136.1Hz may be crowbarred together, but it’s a significantly nonharmonic crowbar.

If we’re after sympathetic and harmonic resonance with 136.1Hz (and thus the Earth’s orbit) we could use that (or its octave equivalents) as a tuning reference (as the Sitar does) or if we want something closer to conventional concert A: 408.3Hz (3/1), 435.52Hz (16/5) 453.66..Hz (10/3) are all more elegant – and consistent with claims to harmonic resonance – than 432Hz.  Not that I am advocating any of these, there is as yet no evidence that 136.1Hz is experientially special, nor has it lived up to any of its claims such as healing, being immune to mechanical noise or the like.

But if you enjoy the idea of being in harmonic resonance with the Earth’s orbit (or any Jupiter’s or Io’s or the 49 Bus schedule for that matter) you should at least be consistent in your aims.

5) Instruments and voices sound better when tuned down to 432Hz

This is the only argument which has real world relevance, though still unconvincing. Acoustic instruments are physical objects, and the tension imparted on their structure has a contribution to the nature of their sound – their timbre – so changing the reference frequency will alter somewhat the timbre of the instrument. The timbre will be different, not necessarily better. For example some guitarists like to ‘downtune’ their instruments for the sound it produces and the looser string feel it provides, but there is no reason for this adjustment to be exactly down to (the impossible to achieve with complete accuracy) 32-odd cent differential. Many adjustments are used, and tuning the guitar all the way down to the next chromatic note in 440Hz tuning was favoured by the not un-cosmic Jimi Hendrix. Note that instruments are designed to sound as good as possible, but they are always adjusted to suit the desires of a player or particular style, and there’s no good argument the changes made by this specific change are in any way better than any other tweak, and there’s no reason to think that – given a 432Hz reference – musicians would suddenly stop making tuning adjustments. Some singers prefer lower tuning systems for the relative ease of vocal production, particularly true when repertoire written for lower systems is tuned to modern concert pitch. However in most circumstances transposing music to lower keys (within a 440Hz reference system) can solve any performance range issues, and still there is no significant relevance or benefit to tuning down by those particular 32ish fractions of a semitone

Now adjusting the tuning by this small amount to synthesizers will create no significant timbral change, and adjusting your music library will in no way make the music more ‘natural’: the timbres will not change, save for perhaps some wholly unnatural artefacts of the adjustment process, and any internal tuning system relationships (for better or worse) will remain identical. If you want to do that to all your music, go for it (you could even play your 33 1/3 LP records at about 32.73 rpm) but rest assured you’re not adjusting the music in any meaningfully significant manner, and any perceived improvements are the results of placebo listening. We humans are hugely suggestible and music is an ideal environment to let those biases run riot.

6) It was an ancient practice from a wiser time

The Earth frequency has been discussed, but there is argument from antiquity based on the claim that 432Hz was previously universally employed Western standard, and presumably superseded by an unwise or malicious musical domination. So here’s a very concise (and far more accurate) history: Prior to the 19^th Century, people made music with no specific – or highly localized – reference pitches. These varied wildly and frequencies given for concert A, as low as around 380Hz and way higher than today’s 440Hz. So much for ancient universal truth. In fact there was a general rise in pitch forged by instrument builder’s arms race – and perhaps deteriorating (and thus shortening) church organ pipes. But as the demand for a shared music practice grew – and singers complained of this pitch inflation – various attempts at standardization arose. Dozens were proposed in the 19^th and 20^th centuries (which varied with region, repertoire and even temperature measurement). Among these were the mid 19^th century ‘Verdi tuning’ of 432Hz (suggested by the composer as a flattening of the prevailing 435Hz French system), and the fairly close to 432Hz ‘scientific tuning’ of C=256Hz (A≈430.54Hz) with its ‘scientific’ basis of C=2^8Hz but these were not particularly favoured among several others. 440Hz itself was formally proposed as early as 1859, so much for the embarrassing Hitler associations (presumably based around a 1939 tuning conference, for which we have no evidence of his association). Even if he happened to like it (for which let’s repeat there is no evidence) there is as much an argument for associating vegetarianism with the Nazis than tuning forks. 440Hz still took till the 1970s for general acceptance, but is still no means universal: Boston Symphony Orchestra use 442Hz, many German and Austrian symphonies use 443Hz and when playing Baroque music, and many ensembles favour the superlow 415Hz. Even rock and pop music – for technological (intended or otherwise) or ad hoc reasons – vary from 440Hz, although less so these days particular with the use of the music technology’s default of 440Hz. However any decent sequencing software and electronic instrument include the ability to deviate from 440Hz (including 432Hz), so those Illuminati need to work harder.

 

Figure 2: Illuminati Fail. I can set my tuning on NWO’s Logic Pro X to 432Hz, and also dial in any temperament. No-one stopped me.

In short as regards reference frequency, there was never an ancient truth, just a glorious diversity (including useful standardisations) which still continues today.

7) The argument from pretty patterns

Many 432Hz proponents claim that cymatics – the vibration patterns of a liquid (usually water) driven by a frequency – lends support to 432Hz superiority over 440Hz (and other) tuning frequencies. Stunning videos of the glaring differences, and the aesthetically more pleasing resulting patterns which 432Hz creates. Here’s the fatal flaw. The patterns produced are dependent on the driving frequency AND the geometry of the container. So some containers will have prettier patterns with a 432Hz rather than a 440Hz, and others might have quite the opposite. The differing wavelengths of 432Hz, 440Hz (and any other frequency) will behave differently in various containers. No 432Hz proponent shows a container that responds well to a 440Hz (although they exist just as readily as ‘432Hz-tuned’ bowls) because that doesn’t fit the a priori conclusion. It’s like arguing that a particular shoe size is perfect by showing a video of  one individual happily walking with one pair, and struggling to put on a different size. Shoes for feet. Horses for courses. Bowls for frequencies.

The Accuracy Issue

There remains a significant pale proboscidea in the room of ‘harmonic’ arguments: There must be some element of acceptable deviation from the harmonic truths, otherwise any microtonal deviation from the pure ratios by unintended human inaccuracy, or intended expression, or even the doppler shift from a slight turn of the listeners head – or temperature fluctuation – will deviate a tuning from harmonic perfection (if ever attainable) of say 3/2 to some crazily irrational proportion ever so slightly higher or lower. I’m a strong advocate of microtonal considerations in music, but I must admit that with a trained musician’s limitation (even in ideal listening conditions) of not much less that 1 cent, along with the laws of physics, means we must take a moderated view to the field. And if one has to make a host of arm-waving concessions to harmonic music, it further undermines any fundamentalist argumentation for the superiority of an arbitrary tuning reference.

In Sum

There’s no particular detriment to moving all music to 432Hz (or any other) tuning, but it’s also entirely possible to engage with music with a variety of tuning reference points, in fact a quick analysis of my music library finds a host of non-440Hz music including pop (Michael Jackson, Beatles), Classical, Renaissance, Jazz, Folk etc. Why advocate the arbitrary homogeneity of 432Hz  when one could have a broad and colourful diversity? Although it’s probable that some advocates are simply tuning all their music down 32-odd cents without checking whether all of it is actually in 440Hz first, making the farce all the more farcical. Most of the claims of the 432-truthers are dubious or fallacious particularly in reference to any superiority or a Musical Truth. If you want to retune your music libraries and instruments go for it, although time is probably better spent investigating any of the many other more pertinent musical dimensions (including – most relevantly – tuning systems).

Musical experience is subjective so if one enjoys 432Hz for whatever reason (even through the placebo effect), that’s fine. But to make real world claims about what is true and what ought to be in music should invite healthy critique and critical thinking and not gullible acceptance and credulous resharing. Speaking of which, if there is a demand, there are a series of controlled listening tests that I am happy to build to investigating any claims of 432Hz superiority while minimizing cognitive biases.

It’s refreshing to see any sort of popular foray into musical analysis, rather than the usual interest in the particular gyratory behaviour of some artist, or the tortured journalism of some sub-sub-sub-genre as a ‘stunning’ revolution. Unfortunately, even with the most generous spirit there’s practically nothing of substance to be found in the 432-truther movement. It seems the only thing discovered is yet another branch of musical pseudoscience, alongside extortionate speaker cables, crystals on speakers and the brown note.

Bonus

As a reward for making it through this post, I offer you some alternatives to 440Hz and 432Hz, feel free to tune your music to any of them (and select whether A, C, C# or whatever note name you invent is the most cosmic) and then start a Facebook group (alongside any manufactured history) to advocate its use.

Pi-tuning 402.1Hz

7 octaves up from Pi, this will add a very rounded and cyclical feel to your music, rather than the square 432Hz and irregular 440Hz

Phi-tuning 414.2Hz

8 octaves above Phi, this is a very balanced tuning, unlike the very disjointed 432Hz and 440Hz.

Selfie Tuning

Perhaps the most personal tuning, simply take the reciprocal of your age in seconds, and multiply it up to a sensible pitch for tuning. For example on your 21st birthday, tune to 414Hz. This results in far more subjective, present music than the materialism of 432Hz and 440Hz. Warning, this will rise, and be prepared to sing like Mariah Carey in your eighties.

Olympic Tuning 272.2Hz

272.2Hz is based on the frequency of the Olympic Games, this produces a more triumphant tuning than 432Hz, with a greater sense of unity than the Earth Frequency.

Galactic Tuning 254.2Hz

65 octaves above the age of the Milky Way, 254.2Hz is way more cosmic than the provincial 432Hz.

Universal Tuning 338.1Hz

67 octaves above the age of the Universe, 338.1Hz is the best tuning reference you can use, and if you don’t agree you must be some kind of Nazi.

I’ll Be Back Tuning 332.7Hz

At 332.7Hz this is 33 octaves above the frequency of Arnold Schwarzenegger movies/per year over the last quarter century. More powerful that 432Hz, and works well with accents.

Bloody Cat Frequency 436.9Hz

This is the most irritating of tuning references: 436.9Hz, a mere 21 octaves above the frequency of my cat waking everyone up in the middle night just to tell us that it’s still raining or that the carpet is in the same position on the floor.

Additional Reading

Benade, Arthur H (1976). Fundamentals of Musical Acoustics. New York: Oxford University Press.

Danielou, Alain (1968). The Ragas of Northern Indian Music. Barrie & Rockliff, London.

Danielou, Alain (1995). Music and the Power of Sound: The Influence of Tuning and Interval on Consciousness. Inner Traditions; Rep Sub edition.

Duffin, R. (2008) How Equal Temperament Ruined Harmony: And Why You Should Care. Paperback edition. Norton.

Fabian D, Timmers R and Schubert E (eds) (2014) Expressiveness in Music Performance: Empirical Approaches Across Styles and Cultures (Oxford University Press)

Fonville, John (1991) “Ben Johnston’s Extended Just Intonation: A Guide for Interpreters”, p.121. Perspectives of New Music 29, no. 2 (Summer): 106–37.

Gann, K (2016) An Introduction to Historical Tunings. http://www.kylegann.com/histune.html

Hans, J. (2001) Cymatics: A Study of Wave Phenomena & Vibration (3rd ed.).

Raichel, D. (2006) The Science and Applications of Acoustics, second edition (Springer).

Skudrzyk, E. (1971) The Foundations of Acoustics: Basic Mathematics and Basic Acoustics (Springer)

Stephens, R. & Bate, A. (1966) Acoustics and Vibrational Physics (2nd ed.). London: Edward Arnold.